気体分子の平均自由行程 - 魔女のちいさな探検

　平均自由行程の計算を書いたサイトを見つけました。

Vacuum Technology (Takagi Ikuji)
　　- 付録A　真空に関係する理論
　　　　A-3　気体分子の平均自由行程

　ここを見ながら、平均自由行程の計算を辿ります。がちがちの計算です(^-^) 結果は[6]です。

　なお、分子は球形に限定です。図を追加しました。

[1] 1成分系、止まった球の中を飛ぶ球
[2] 1成分系、すべての球が同じ速さで運動、向きはランダム
[3] 1成分系、マクスウェルの速度分布関数
[4] 2成分系、それぞれ一定の速さ
[5] 2成分系、マクスウェルの速度分布関数
[6] 空気の場合
[7] その他

[1] 1成分系、止まった球の中を飛ぶ球

　気体分子の数密度を n 、これがすべて静止しています。この中を速さ v で飛ぶ分子があります。衝突後飛び始めてから次に衝突するまでを図のように考えます。

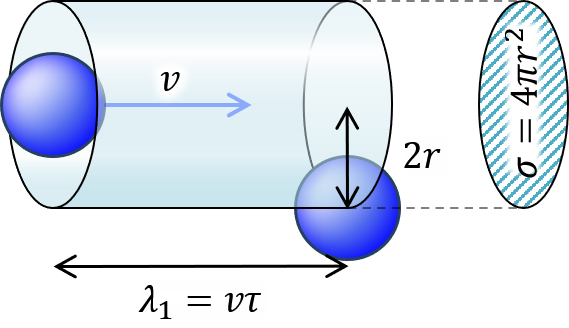
　　分子の半径　　 r
　　全散乱断面積　 σ = 4 π r^2　　　　　　　　　　　　　　　　　　　(1)
　　平均自由時間　 τ
　　平均自由行程　λ = v τ　　　　　　　　　　　　　　　　　　　　　　(2)

　1分子当たりの体積を λ σ と考えれば、

　　λ σ = 1 / n　　　　　　　　　　　　　　　　　　　　　　　　　　　(3)
　　λ = 1 / (n σ) = 1 / (n 4 π r^2)　　　　　　　　　　　　　　　　　　　(4)

平均自由行程には分子の大きさ 2r が出てきます。

[2] 1成分系、すべての球が同じ速さで運動、向きはランダム

　注目する分子1と、最初に衝突する分子2を考えます。分子2が静止する座標系にすれば、[1] の計算が使えます。
　分子1の速度を v_1 、分子2の速度を v_2 、相対速度を u とします。太字はベクトルです。

　　u = v_1 - v_2　　　　　　　　　　　　　　　　　　　　　　　　　　( )

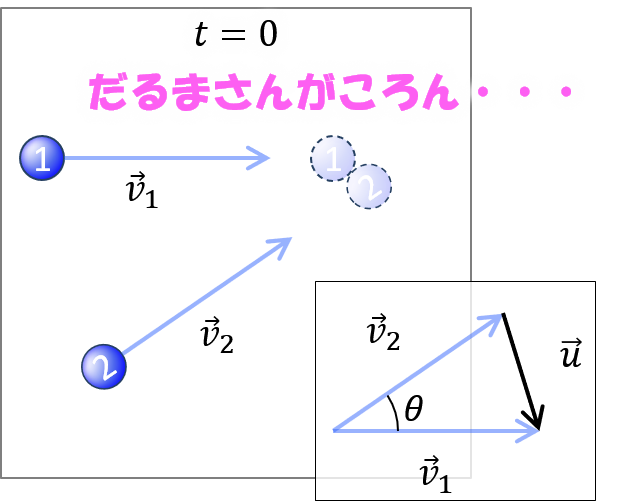
相対速度の平均値 u を計算します。

　　u ≡ (<u^2>)^(1/2)　　　　　　　　　　　　　　　　　　　　　　　( )

　　u^2 = v_1^2 + v_2^2 - 2 v_1 v_2 cosθ　　　　　　　　　　　　　　　(5)

ここで、すべての球の速さを一定の v とします。2つの分子の運動方向はランダムだから、角度 θ の平均は 0 です。

　　u^2=2 v^2　　　　　　　　　　　　　　　　　　　　　　　　　　　(6)

次に、分子2が静止して見える座標系に移行します。この u を (2) の v の部分に代入して、

　　λ' = u τ　　　　　　　　　　　　　　　　　　　　　　　　　　　　( )

当たった瞬間のその他の分子の配置は、ランダムだと想定して、

　　λ' = 1 / n σ , 　　v τ = 1 / (2^(1/2) n σ)　　　　　　　　　　　　　　(7)

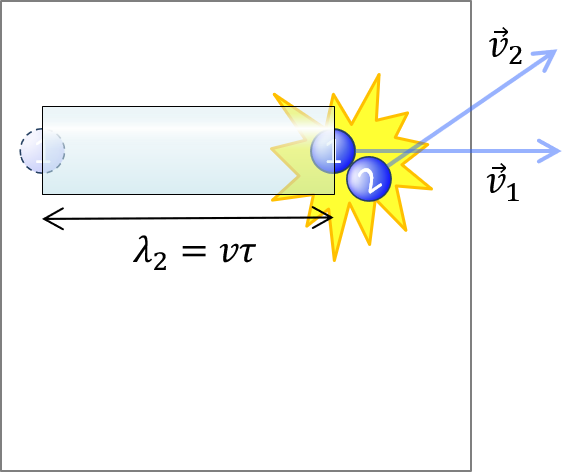
もとの座標系に戻ると、平均自由時間 τ はそのままで、分子1の速度は v_1 に戻ります。平均自由行程 λ は

　　λ = v τ = 1 / (2^(1/2) n σ)　　　　　　　　　　　　　　　　　　　　(8)

1/√(2) ほど短くなります。
　1次元で考えると両脇の分子が動いていると自分の領域が少し小さくなるので、まあ良さそうです。

[3] 1成分系、マクスウェルの速度分布関数

　1分子の速度の分布関数を

　　F(v) = (a / π)^(3/2) exp (- a v^2)　,　　a = m / (2 k_B T)　　　　　　(9)

相対速度は

　　<(v_1 - v_2)^2> = ∫dv_1∫dv_2 (v_1 - v_2)^2 F(v_1)F(v_2)　　　　　(10)

　　　　　　　　　= 2<v^2> = u^2　　　　　　　　　　　　　　　　　(11)

ガウス積分で、

　　<v^2> = 3 / (2a) = 3 k_B T / m　　　　　　　　　　　　　　　　　(12)

平均自由行程は (8) と同じで

　　λ = v τ = 1 / (2^(1/2) n σ)　　　　　　　　　　　　　　　　　　　(14)

速さ一定の場合と同じ結果になります。また、速さは質量と温度で表せます。

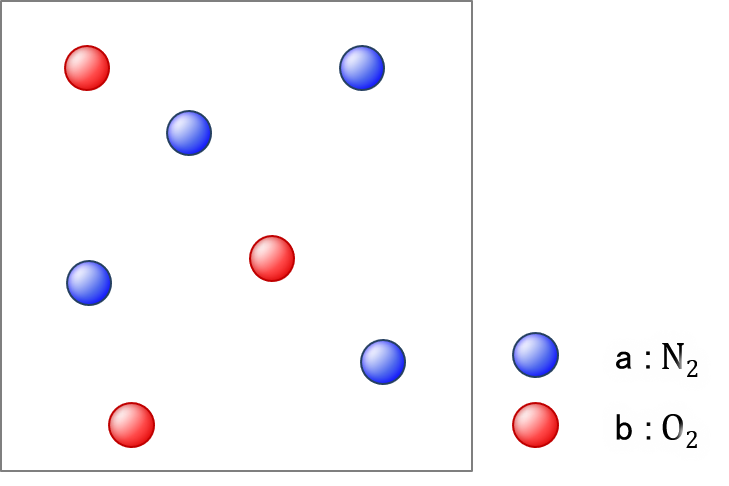
[4] 2成分系、それぞれ一定の速さ

　いよいよ知りたかった部分です。2種類の分子a、bがあるとします。分子a、分子bは、それぞれ一定の速度で飛んでいるとします。

　計算の方針としては、分子の衝突頻度を求めて、この合計から平均自由時間を求めます。

　まず、分子aが同種の分子aに衝突する頻度は、(8) より、

　　1 / τ_{aa} = 2^(1/2) v_a n_a σ_a 　　　　　　　　　　　　　　　　　(15)

　分子aが分子bに衝突する頻度は、相対速度の部分を再計算します。

　　u = v_a - v_b　　　　　　　　　　　　　　　　　　　　　　　　　( )
　　u^2 = v_a^2 + v_b^2　　　　　　　　　　　　　　　　　　　　　　(17)

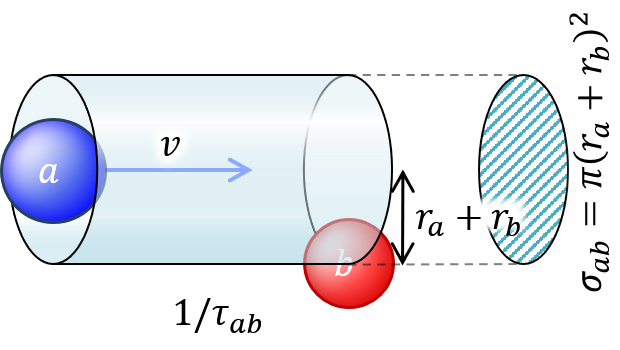
あとは [2] と同じ手順で

　　1 / τ_{ab} = (v_a^2 + v_b^2)^(1/2) n_b σ_{ab} 　　　　　　　　　　　(19)
　　σ_{ab} = π (r_a + r_b)^2　　　　　　　　　　　　　　　　　　　　　(17b)

分子aの全衝突頻度は (15) + (19) で、

　　1 / τ_a = 2^(1/2) v_a n_a σ_a + (v_a^2 + v_b^2)^(1/2) n_b σ_{ab} 　　(20)

平均自由行程は

　　λ_a = v_a τ_a　　　　　　　　　　　　　　　　　　　　　　　　　(21)

分子bに関しては、添え字のaとbを入れ替えた形になります。

[5] 2成分系、マクスウェルの速度分布関数

　[4] (20)、(21)式の速さの部分に、[3] (12) 式の平均速さをそのまま入れます。平均自由行程は数密度と質量で表現できます。

　　λ_a = 1 / [ 2^(1/2) n_a σ_a + (1 + m_a / m_b)^(1/2) n_b σ_{ab} ] 　　(22)
　　λ_b = 1 / [ 2^(1/2) n_b σ_b + (1 + m_b / m_a)^(1/2) n_a σ_{ab} ] 　　(23)

それぞれの全散乱断面積は、

　　σ_a = 4 π r_a^2　　　　　　　　　　　　　　　　　　　　　　　　(1)
　　σ_b = 4 π r_b^2 = (r_b / r_a)^2 σ_a 　　　　　　　　　　　　　　　(1)'
　　σ_{ab} = π (r_a + r_b)^2 = (1 + r_b / r_a)^2 / 4 × σ_a　　　　　　　　(17b)

平均自由行程の計算に必要なパラメータは、密度、分子の大きさ、質量になります。

[6] 空気の場合

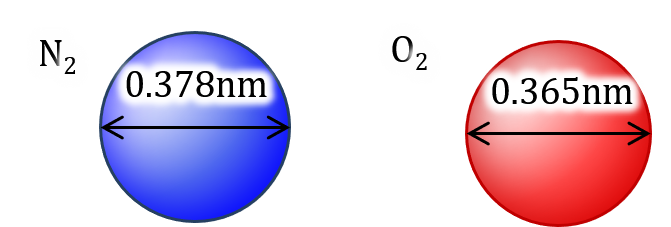
　空気の平均自由行程を計算します。a を窒素、b を酸素とします。

　　m_a / m_b = 0.875　　　　　　　　　　　　　　　　　　　　　　(24a)
　　2r_a = 3.78×10^(-10) [m] (参考)　　　　　　　　　　　　　　　　　(24b)

　　r_b / r_a = 0.966 　　　　　　　　　　　　　　　　　　　　　　(24c)
　　σ_{ab} = (1 + r_b / r_a)^2 / 4 × σ_a = 0.9659 σ_a 　　　　　　　　(24d)
　　σ_b = (r_b / r_a)^2 σ_a = 0.9332 σ_a 　　　　　　　　　　　　　　(24e)
　　σ_a = 4 π r_a^2 = 44.89×10^(-20) [m^2]　　　　　　　　　　　(24f)

平均自由行程は、

　　1 / λ_a = σ_a (1.41 n_a + 1.32 n_b)　　　　　　　　　　　　　　　(27)
　　1 / λ_b = σ_a (1.41 n_a + 1.32 n_b)　　　　　　　　　　　　　　　(28)

酸素と窒素で偶然の一致です！地表の標準大気では

　　T = 288 [K] , P = 101325 [Pa]　　　　　　　　　　　　　　　　　　(24g)
　　n_0 = P/(k_B T) = 2.55×10^25 [m^(-3)]　　　　　　　　　　　　　(24h)
　　n_0 σ_a = 1.144×10^7 [m^(-1)]　　　　　　　　　　　　　　　　　　(24i)
　　n_a = 0.781 n_0 , n_b = 0.210 n_0　　　　　　　　　　　　　　　　　(24j)

　空気は、ほぼ酸素と窒素の混合気体として、n_b = n_0 - n_a と変えます。(27)、(28)式に代入して、平均自由行程は、

　　1 / λ = 1.1×10^7 × (1.41 n_a / n_0 + 1.32 n_b / n_0) [m^(-1)]　　　　(29)

　―――――――――――――――――――――――――――――――
　　窒素の割合 n_a / n_0 [%]　　　平均自由行程 λ [nm]
　―――――――――――――――――――――――――――――――
　　　　　100　　　　　　　　　　　　　　64
　　　　　 78.1 　　　　　　　　　　　　　 65
　　　　　　0　　　　　　　　　　　　　　69
　―――――――――――――――――――――――――――――――
まあまあな結果です。窒素のみでも酸素のみでも、ほぼ同じオーダーです。出典では窒素100%、30℃1気圧で 67 [nm] となりますが、気温が高い分密度は低くなっています。

　大気が窒素100%で熱平衡の場合、上空の分子密度 n(z) は

　　n(z) = n_0 exp (- z / z_0)　　　　　　　　　　　　　　　　　　　　(10-8)

気温を-40℃の一定として、

　　z_0 = 7.06 [km]　　　　　　　　　　　　　　　　　　　　　　　　(10-8)下

とすれば、
　―――――――――――――――――――――――――――――――
　　　　高度 z [km]　　　　　平均自由行程 λ
　―――――――――――――――――――――――――――――――
　　　　　　0　　　　　　　　　　　　64 [nm]
　　　　　 80 　　　　　　　　　　　 5.4 [mm]
　―――――――――――――――――――――――――――――――
上空では単位が違います。